| |
 "РАВНОВЕЛИКИЕ ФИГУРЫ"
"РАВНОВЕЛИКИЕ ФИГУРЫ"
Скажи мне – и я забуду,
Покажи мне – и я запомню,
Вовлеки меня – и я пойму.
Древняя китайская мудрость
|
Цели урока:
Оборудование: Мультимедиа проектор, программное обеспечение: «Интерактивная математика 5 – 9 класс». Дрофа – ДОС Мультимедиа, 1 С: Образовательная коллекция «Планиметрия 7 - 9»; ножницы, угольники, линейки, модели произвольных треугольников, простые карандаши, квадрат «Танграм» (всего 15 комплектов); кусочки двустороннего скотча для наклеивания частей фигуры; листы белой бумаги; демонстрационный материал – решение задачи.
ХОД УРОКА
 
I. Организационный момент
Учитель:
Как вы думаете, какова цель сегодняшнего урока? (учащиеся формулируют цель урока).
Ещё можно дополнить сформулированную цель урока следующим: познакомится с понятием равносоставленных фигур, вывести формулы площадей параллелограмма и треугольника.
Сообщение темы и цели урока.
II. Формирование новых понятий и способов действий
 1. Введение понятия равносоставленных и равновеликих фигур.
А начнём мы изучать новый материал с решения проблемы.
1. Введение понятия равносоставленных и равновеликих фигур.
А начнём мы изучать новый материал с решения проблемы.
|
|
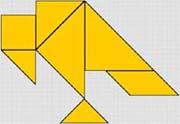
На экране одноцветная фигура «Танграм» [1]
(«Интерактивная математика 5-9» Площади фигур.)
Вопрос. Как найти площадь данной фигуры, изображающей силуэт птицы?
Возможный вариант ответа:
Разрезать данную фигуру на известные геометрические фигуры, найти сумму их площадей.
Учитель. Да, вы правы, необходимо, разрезать эту «птицу» на известные геометрические фигуры, и попытаться найти площадь каждой.
Действия учителя. Учитель разбирает «птицу» на части и меняет их цвет.
|

|
Вопрос. Теперь мы видим, что эта фигура являлась «хитроумным узором из семи частей», но возникает опять проблема: как, же нам вычислить площадь каждой части, если нам известна только формула площади квадрата или прямоугольника?
Возможный вариант ответа:
Необходимо попытаться собрать эти семь частей в квадрат.
Учитель. Да, действительно, необходимо собрать эти семь фигур в квадрат, называемый в древнем Китае «Доска Мудрости».
Действия учителя. Учитель собирает семь геометрических фигур в квадрат.
Учитель. Мы только, что увидели, что и данная фигура, и квадрат составлены из одних и тех же геометрических фигур.
|
Такие фигуры называются равносоставленными.
А что вы можете сказать о площадях этих фигур? Да, площади равносоставленных фигур равны, а фигуры, имеющие равные площади называются равновеликими.
Вывод. Из всего вышесказанного можно сформулировать свойство площади: если фигура составлена из нескольких фигур, то её площадь равна сумме площадей этих фигур.
|
 2. Вывод формул площадей параллелограмма и треугольника.
2. Вывод формул площадей параллелограмма и треугольника.
1) Вывод формулы площади параллелограмма.
|

|
Учитель. Используя, выше сформулированное свойство площади, выведем формулы площадей параллелограмма. Для этого «перекроим» параллелограмм в прямоугольник.
Учитель в этой же программе составляет из параллелограмма прямоугольник.
Вопрос.
С помощью, какой формулы можно вычислить площадь параллелограмма?
Ответ. S = ah.
Площадь параллелограмма равна произведению высоты и стороны, к которой, проведена эта высота.
|
|
Замечание. В случае необходимости, в этом же кадре, начертить параллелограмм и провести его высоту.
|
2) Вывод формулы площади треугольника.
Работа в парах.
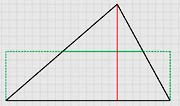
Творческое задание «Голова хорошо, а две – лучше». Разрежьте треугольник на части и составьте из них прямоугольник. Сделайте вывод о формуле площади этого треугольника.
|
|
Задание. Объясните способ разрезания треугольника на части.
Варианты ответа.
1. Опустить высоту из вершины треугольника к противолежащей стороне.
2. Провести среднюю линию треугольника, соединяющую середины двух других сторон. Эта средняя линия отсечёт от данного треугольника два треугольника, которые необходимо отрезать и приставить к третьей стороне рассматриваемого треугольника.
|
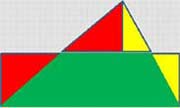
|
Действия учителя. На экране демонстрируется решение данной задачи.
Вывод:
Площадь треугольника равна половине произведения его высоты и стороны, на которую опущена эта высота.
S =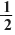 ah. ah.
|
III. Применение знаний, формирование умений и навыков
Замечание. Подготовить диск ОК с программой «Планиметрия 7 – 9».
Закрепим понятие равновеликих фигур и формулы площади треугольника при помощи практической работы.
Практическая работа «Дорогу осилит идущий».
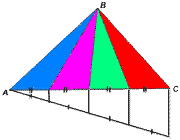
Задание. Разделите треугольник на три (четыре) равновеликих треугольника.
Вам понадобятся чертежные инструменты!
|
1 вариант
На три равновеликих
треугольника.

|
2 вариант
На четыре равновеликих треугольника.
Инструктаж. При выполнении этой практической работы вам понадобится алгоритм деления данного отрезка на n равных частей. Обратимся к этой задаче помощи специальной компьютерной программы.
Вход в программу (или выйти на нужную тему и задачу через «закладку»).
Учебник. Раздел.
ГМТ и геометрические построения.
Тема.
Построения циркулем и линейкой.
Задачи.
Деление отрезка на n равных частей.
|
2. Проверка результатов выполнения практической работы.
|
|
Учитель. Расскажите, каким образом вы разделили данный треугольник на равновеликие треугольники. Обоснуйте свой ответ.
Решение данной задачи.
Необходимо одну из сторон данного треугольника разделить на n равных частей, затем соединить противолежащую вершину с отмеченными точками на стороне.
|
IV. Первичный контроль за усвоением знаний
Практическая работа «Где руки и охота, там спорая работа».
Задание. Соберите одну фигурку «Танграм».
|
Дал Бог руки, а веревки сам вей!
|

|
|
Домашнее задание. Найди площадь составленной фигурки «Танграм».
|
V. Итог урока
Информационные ресурсы:
1. «Интерактивная математика 5 – 9 класс». Дрофа – ДОС Мультимедиа.
2. 1 С: Образовательная коллекция «Планиметрия 7 - 9».
|
 "РАВНОВЕЛИКИЕ ФИГУРЫ"
"РАВНОВЕЛИКИЕ ФИГУРЫ"

 Введение понятия равновеликих фигур, вывод формул площади параллелограмма и треугольника; формирование конструктивного мышления, умений и навыков решения задач на применение введённых понятий и формул площадей;
Введение понятия равновеликих фигур, вывод формул площади параллелограмма и треугольника; формирование конструктивного мышления, умений и навыков решения задач на применение введённых понятий и формул площадей;
 1. Введение понятия равносоставленных и равновеликих фигур.
1. Введение понятия равносоставленных и равновеликих фигур.




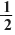 ah.
ah.

