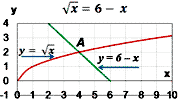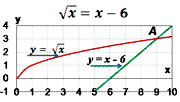| |
 "ФУНКЦИЯ
"ФУНКЦИЯ 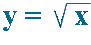 И ЕЁ ГРАФИК" И ЕЁ ГРАФИК"
Сажи мне – и я забуду,
Покажи мне – и я запомню,
Вовлеки меня – и я пойму.
Древняя китайская мудрость
|
Цели урока:
Оборудование: мультимедиа проектор, диск «Интерактивная математика 5 – 9 класс». Дрофа – ДОС Мультимедиа; демонстрационный материал; график функции  . .
ХОД УРОКА
I. Организационный момент
II. Д/З п.15; стр. 82; № № 362 (б); 368 (а); 367; 359.
III. Проверка домашнего задания: №№ 364 (вгд); 365 (бг); 366 (вг).
№ 364. Сравните числа:
a)  27 и 27 и  28; 28;
б)  1.3 и 1.3 и  1.5; 1.5;
в)  7 и 3; 7 и 3;
г)  6.25 и 2.5; 6.25 и 2.5;
д) 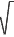 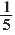 и и  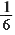 ; ; |
№ 365. Расположите
в порядке возрастания числа:
a)  2.3, 2.3,  10.4 и 10.4 и  19.5; 19.5;
б)  18, 18,  12 и 4; 12 и 4;
в) 0.5,  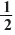 и и  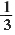 ; ;
г)  0.7, 0.7,  1.7 и 1; 1.7 и 1; |
№ 366. Найдите значение выражения.
в)  400 - (4 400 - (4 0.5)2; 0.5)2;
г) (-3 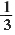 )2 - 10; )2 - 10;
|
IV. Актуализация опорных знаний учащихся и их коррекция
|
1. Устные упражнения (фронтальная работа)
|
|
1. Какие элементарные функции вам известны. Задайте их общей формулой.
|
|
2. График, какой функции:
(на доске стрелками показать соответствие)
|
y = x2; y = x3; y = 3 x; y = x - 2; y = 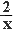 ; y = ; y =  x; y = x; y =  ;
является гиперболой; параболой; кубической параболой; прямой; полупараболой? ;
является гиперболой; параболой; кубической параболой; прямой; полупараболой?
|
|
3. Расскажите, как построить графики известных вам функций.
|
|
4. Расскажите приём графического решения уравнения:
Учащиеся формулируют состав приёма графического решения уравнения.
|
 x = x = 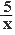 ; ;
|
|
Решение демонстрируется на экране при помощи программы «Интерактивная математика 5 – 9 класс». Дрофа – ДОС Мультимедиа, «Графики уравнений и неравенств».
Перед демонстрацией включить «Помощник», который расскажет о работе программы.
|
 Строим графики функций: y = Строим графики функций: y =  x и y = x и y = 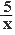 . .
 Находим абсциссы общих точек построенных графиков, это и будет являться решением данного уравнения. Находим абсциссы общих точек построенных графиков, это и будет являться решением данного уравнения.
Ответ: x  3. 3.
Замечание. По ходу решения уравнения задавать вопросы.
|

|
5. Составьте уравнение, с использованием функции вида y =  x других функций (например, из устных упражнений). Уравнение написать на доске.
Решите его графически при помощи программы «Интерактивная математика 5 – 9 классы». x других функций (например, из устных упражнений). Уравнение написать на доске.
Решите его графически при помощи программы «Интерактивная математика 5 – 9 классы».
|
V. Применение знаний, совершенствование умений и навыков
№ 361. Какой из графиков линейных функций не пересекает графика функции y =  x ? x ?
1. y = -x + 2; 2. y = - x + 0,1; 3. y = - x; 4. y = -x – 0,1.
|
Ответ: № 4
|
Коллективная работа:
Решить уравнение 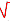 x + x - 6 = - 5 x + x - 6 = - 5
 x = - x + 1 x = - x + 1
Строим графики функций: y =  x и y = - x + 1 x и y = - x + 1
Находим абсциссы общих точек построенных графиков, это и будет являться решением данного уравнения.
Ответ: x  0,43 0,43
|

|
Индивидуальная работа:
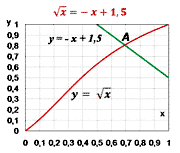
Решить уравнение 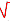 x = - x + 1.5 x = - x + 1.5
Строим графики функций: y =  x и y = - x + 1.5 x и y = - x + 1.5
Находим абсциссы общих точек построенных графиков, это и будет являться решением данного уравнения.
Ответ: x  0,69 0,69
|
|
№ 360. Имеют ли общие точки графики функций:
a) y =  x и y = x; x и y = x;
б) y =  x и y = 1000; x и y = 1000;
в) y =  x и y = x + 10; x и y = x + 10;
г) y =  x и y = - x + 1.5; x и y = - x + 1.5;
При положительном ответе укажите координаты этих точек.
|
Решение:
а) Да. А (0; 0), В 3(1; 1).
б) Да. А (106; 103).
в) Нет.
г) Да. А (0,7; 0,8).
|
VI. Контроль (проверочная разноуровневая самостоятельная работа)
I ВАРИАНТ Решите графически уравнение:
1)  x = 6 - x;
2) x = 6 - x;
2)  x = x2;
3) x = x2;
3)  x = x = 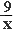 ; ;
Ответы:
1) x = 4;
2) x1 = 0; x2 = 1;
3) x  4.2; 4.2;
|
II ВАРИАНТ Решите графически уравнение:
1)  x = x - 6;
2) x = x - 6;
2)  x = x3;
3) x = x3;
3)  x = x =  ; ;
Ответы:
1) x = 9;
2) x1 = 0; x2 = 1;
3) x = 4;
|
|
Критерии оценки: «3» - № 1; «4» - № 2; «5» - № 2; 3.
|
VII. Итог урока.
Самопроверка результатов и выставление самооценок. На обратной стороне доски открываются верные результаты. Можно воспользоваться интерактивной программой.
Самостоятельная работа
I ВАРИАНТ Решите графически уравнение:
1)  x = 6 - x;
Ответ:
x = 4; x = 6 - x;
Ответ:
x = 4;
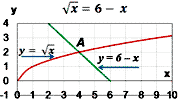
|
II ВАРИАНТ Решите графически уравнение:
1)  x = x - 6;
Ответ:
x = 9; x = x - 6;
Ответ:
x = 9;
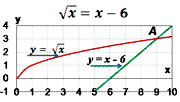
|
Решите графически уравнение:
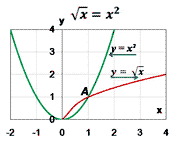
2)  x = x2;
Ответ:
x1 = 0; x2 = 1; x = x2;
Ответ:
x1 = 0; x2 = 1;
|
Решите графически уравнение:
2)  x = x3;
Ответ:
x1 = 0; x2 = 1; x = x3;
Ответ:
x1 = 0; x2 = 1;

|
Решите графически уравнение:
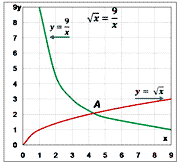
3)  x = x = 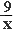 ;
Ответ:
x ;
Ответ:
x  4.2; 4.2;
|
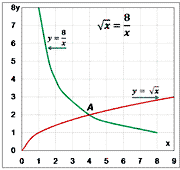
Решите графически уравнение:
3)  x = x =  ;
Ответ:
x = 4; ;
Ответ:
x = 4;
|
|
Критерии оценки: «3» - № 1; «4» - № 2; «5» - № 2; 3.
|
|
 "ФУНКЦИЯ
"ФУНКЦИЯ 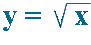 И ЕЁ ГРАФИК"
И ЕЁ ГРАФИК" .
. Закрепление понятия функции, совершенствование умений учащихся строить график введённой функции и применять её свойства при решении задач; повторение приёма графического решения уравнения.;
Закрепление понятия функции, совершенствование умений учащихся строить график введённой функции и применять её свойства при решении задач; повторение приёма графического решения уравнения.;
 27 и
27 и 
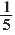 и
и 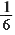 ;
; 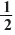 и
и 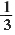 ;
; 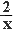 ; y =
; y =  ;
является гиперболой; параболой; кубической параболой; прямой; полупараболой?
;
является гиперболой; параболой; кубической параболой; прямой; полупараболой?
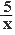 ;
; 3.
3.

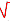 x + x - 6 = - 5
x + x - 6 = - 5


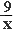 ;
;
 ;
;