| |
 "Логарифмическая функция и её приложения"
"Логарифмическая функция и её приложения"
Потому-то словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Борис Слуцкий
|
Цели урока:
 повторить свойства логарифмической функции; повторить свойства логарифмической функции;
 обобщить, систематизировать и углубить знания по данной теме; обобщить, систематизировать и углубить знания по данной теме;
 расширять представления учащихся о логарифмической функции, применении ее свойств в нестандартных ситуациях; расширять представления учащихся о логарифмической функции, применении ее свойств в нестандартных ситуациях;
 развивать интерес к истории математики и ее практическим приложениям, логическое мышление, математическую грамотность речи; развивать интерес к истории математики и ее практическим приложениям, логическое мышление, математическую грамотность речи;
 воспитывать познавательную активность, чувство ответственности, культуру общения, культуру диалога. воспитывать познавательную активность, чувство ответственности, культуру общения, культуру диалога.
Оборудование: компьютер, мультимедийная презентация, логарифмическая линейка, таблица логарифмов.
ХОД УРОКА
  
 
I. Организационный момент
Здравствуйте! Как Ваше настроение? Настроены ли Вы на работу? Все ли принадлежности приготовлены к уроку? Тогда в добрый путь! Улыбнемся друг другу!
Сообщение темы и цели урока.
II. Актуализация опорных знаний
1. Театрализованный эпизод «Суд над логарифмами»
Секретарь:
Встать, суд идет!
Прошу всех сесть.
Судья:
Этот человек утверждает,
Что логарифмы не нужны.
И их не применяют.
Слово предоставляю прокурору:
Объясните суть спора.
Прокурор:
Наш подсудимый глупо рассуждает,
Истории, к тому же он не знает!
Веками люди над их открытием трудились,
Облегчить вычисления стремились.
С тем логарифм и был изобретен,
И функция придумана потом.
Судья:
Свидетелям теперь я слово предоставлю,
Их показания без внимания не оставлю.
|
1-й свидетель:
Друзья, поверьте:
самая интересная, полезная и лирическая
Это – функция логарифмическая.
Спросите вы: «А чем интересна?»
А тем, что обратна она показательной
И относительно прямой y = x, как известно,
Симметричны их графики обязательно.
2-й свидетель:
Проходит график через точку (1;0)
И в том еще у графика соль,
Что в правой полуплоскости он «стелется»,
А в левую попасть и не надеется.
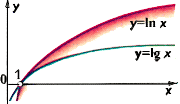
3-й свидетель:
Но, если аргументы поменяем,
Тогда по правилам кривую мы сдвигаем,
Растягиваем, если надо, иль сжимаем
И относительно осей отображаем.
Сама же функция порою убывает,
Порою по команде возрастает.
А командиром служит ей значенье 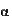 , ,
И подчиняется она ему всегда.
|
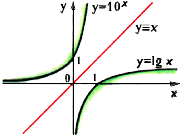
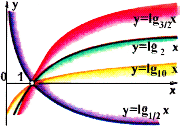
|
2. Устные упражнения.
Прочитайте: loga b
1) Каким должно быть число 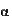 , каким число b? , каким число b?
2) Какой логарифм называется десятичным?
3) Какой логарифм называется натуральным?
|
Из данных функций назовите логарифмическую:
y=4x; y=log5 25+x2;
y=ln(x+2);
y=2.5x; y=log5 125+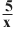 ; ;
|
Какой график является графиком функции y=log0.4 x?
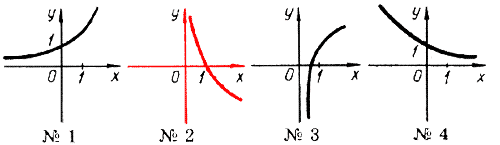
|
Совпадают ли графики функций ?
f(x)=x+1 и
g(x)=2log2(x+1)
Ответ обоснуйте.
1. ДА 2. НЕТ
|
При каких значениях х имеет смысл выражение
log0.5 (log2 x)?
1. При любом значении х;
2. При положительном значении х;
3. При х > 1;
4. При 0 < x < 1.
|
Найдите область определения функции y=log2 (5-3х).
1. { -1 ; + ; +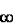 }
2. { - }
2. { -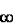 ; -1 ; -1 }
3. { 1 }
3. { 1 ; + ; +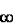 }
4. { - }
4. { -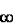 ; 1 ; 1 } }
|
Самостоятельная работа. Вычислите :
Вариант 1. log2128; log5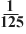 ; log327; log77; log51; ; lg0,0001; lg100000. (7, -3, 3, 1, 0, -4, 5) ; log327; log77; log51; ; lg0,0001; lg100000. (7, -3, 3, 1, 0, -4, 5)
Вариант 2. log232; log2 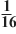 ; log464; log31; lg10; lg0,001; lg1000000. (5, -4, 2, 0, 1, -3, 6) ; log464; log31; lg10; lg0,001; lg1000000. (5, -4, 2, 0, 1, -3, 6)
|
Учитель: Итак, мы повторили свойства логарифмической функции.
Расширим наши представления о логарифмической функции и применим ее свойства в нестандартных ситуациях.
III. Сообщения учащихся по теме урока и решение нестандартных заданий
1. Ода экспоненте.

Поистине безграничны приложения показательной и логарифмической функций в самых различных областях науки и техники, а ведь придумывали логарифмы для облегчения вычислений. Через пять лет будет четыре столетия с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные Джоном Непером. Они помогли астрономам и инженерам, сокращая время на вычисления, и тем самым, как сказал знаменитый французский ученый Лаплас, «удлиняли жизнь вычислителям».
 Еще недавно трудно было представить инженера без логарифмической линейки в кармане; изобретенная через десяток лет после появления логарифмов Непера английским математиком Гунтером, она позволяла быстро получать ответ с достаточной для инженера точностью в три значащие цифры. Теперь ее из инженерного обихода вытеснили микрокалькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни калькуляторы.
Еще недавно трудно было представить инженера без логарифмической линейки в кармане; изобретенная через десяток лет после появления логарифмов Непера английским математиком Гунтером, она позволяла быстро получать ответ с достаточной для инженера точностью в три значащие цифры. Теперь ее из инженерного обихода вытеснили микрокалькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни калькуляторы.
Многообразие применения показательной (или как ее еще называют экспоненциальной) функции вдохновили английского поэта Элмера Брила, он написал «Оду экспоненте»:
«…Ею порождено многое из того,
Что достойно упоминания»,
Как говорили наши
Англосаксонские предки.
Могущество ее порождений
Заранее обусловлено ее
Собственной красотой и силой,
Ибо они суть физическое воплощение
Абстрактной идеи ее.
Английские моряки любят и знают ее
Под именем «Гунтер».
|
Две шкалы Гунтера –
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?
И таким образом абстрактно красивое
Стало предком одного из величайших
Человеческих достижений».
|
Учитель: Были поэты, которые не посвящали од экспоненте и логарифмам, но упоминали их в своих стихах. Например, в своем стихотворении «Физики и лирики» поэт Борис Слуцкий написал те строки, которые вынесены в эпиграф к уроку (записаны на доске).
Задание 1.
Построить график функции: 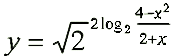
Решение
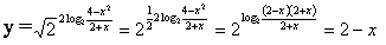 ОДЗ: ОДЗ: 
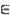 ( - ( - 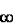 ; - 2 ) U (- 2; 2) ; - 2 ) U (- 2; 2)
y = 2 - x
x 0 1
y 2 1
2. «Логарифмы в музыке»
Музыканты редко увлекаются математикой; большинство из них питают к этой науке чувство уважения. Между тем, музыканты - даже те, которые не проверяют подобно Сальери у Пушкина («алгеброй гармонию»), - встречаются с математикой гораздо чаще, чем сами подозревают, и притом с такими «страшными» вещами, как логарифмы.
  Известный физик Эйхенвальд вспоминал: «Товарищ мой по гимназии любил играть на рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом не имеют ничего общего. «Правда, Пифагор нашел какие-то соотношения между звуковыми колебаниями, - но ведь как раз пифагорова-то гамма для нашей музыки и оказалась неприемлемой». Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах...»
Известный физик Эйхенвальд вспоминал: «Товарищ мой по гимназии любил играть на рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом не имеют ничего общего. «Правда, Пифагор нашел какие-то соотношения между звуковыми колебаниями, - но ведь как раз пифагорова-то гамма для нашей музыки и оказалась неприемлемой». Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах...»
И действительно, так называемые ступени 12-звуковой гаммы частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях).
Задание 2.
Решите уравнение: tg 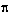 x log3( x log3(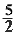 x - x 2) = 0 (Пшукова Назират) x - x 2) = 0 (Пшукова Назират)
Решение
tg 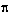 x = 0; или x = 0; или
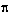 x = arctg0 + x = arctg0 + 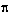 k, k,
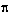 x = x = 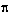 k, k,
x = k,
если k=1, то х=1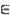 ОДЗ, ОДЗ,
если k=2, то х=2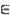 ОДЗ. ОДЗ.
Ответ: 1; 2
|
log3(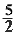 x - x 2) = 0, x - x 2) = 0,
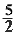 x - x 2 = 1, x - x 2 = 1,
x2 - 2.5х + 1 = 0,
х1 = 2, х2 = 0.5
2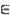 ОДЗ, 0.5 ОДЗ, 0.5 ОДЗ ОДЗ
|
ОДЗ:
1) 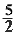 x - x 2 > 0, x (2.5 - x) > 0, x - x 2 > 0, x (2.5 - x) > 0,
x 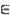 (0; 2.5) (0; 2.5)
2) cos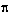 x x  0 0 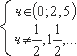
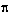 x x   + + 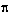 k k
x   + k; x + k; x  0.5; 1.5; 2.5 0.5; 1.5; 2.5
|
3. Звезды, шум и логарифмы
Этот заголовок связывает столь, казалось бы, несоединимые вещи. Шум и звезды объединяются здесь потому, что громкость шума и яркость звезд оцениваются одинаковым образом - по логарифмической шкале.
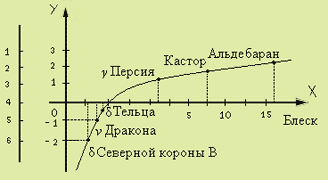  Астрономы делят звезды по степени яркости на видимые и абсолютные звездные величины - звезды первой величины, второй, третьей и т. д. Последовательность видимых звездных величин, воспринимаемых глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону: яркости звезд составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой логарифм ее физической яркости. Короче говоря, оценивая яркость звезд, астроном оперирует таблицей логарифмов, составленной при основании 2,5.
Астрономы делят звезды по степени яркости на видимые и абсолютные звездные величины - звезды первой величины, второй, третьей и т. д. Последовательность видимых звездных величин, воспринимаемых глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону: яркости звезд составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой логарифм ее физической яркости. Короче говоря, оценивая яркость звезд, астроном оперирует таблицей логарифмов, составленной при основании 2,5.
Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и на производительность труда побудило выработать приемы точной числовой оценки громкости шума. Единицей громкости звука служит «бел», но практически используются единицы громкости, равные его десятой доле, - так называемые «децибелы».
Последовательные степени громкости 1 бел, 2 бела и т.д. составляют арифметическую прогрессию... Физические же величины, характеризующие шумы (энергия, интенсивность звука и др.), составляют геометрическую прогрессию со знаменателем 10. Громкость, выраженная в белах, равна десятичному логарифму соответствующей физической величины.
4. Физкультминутка.
5. Логарифмическая «комедия» 2 > 3
Комедия начинается с неравенства  > >  , бесспорно правильного. Затем следует
преобразование, тоже не внушающее сомнения. Большему числу соответствует больший логарифм, , бесспорно правильного. Затем следует
преобразование, тоже не внушающее сомнения. Большему числу соответствует больший логарифм,
значит, lg( )2 > lg( )2 > lg( )3 , 2lg )3 , 2lg  > 3lg > 3lg  . .
После сокращения на lg имеем 2 > 3. имеем 2 > 3.
В чем ошибка этого доказательства? (т.к. lg < 0, то при сокращении меняем знак на <). < 0, то при сокращении меняем знак на <).
6. Сообщение «Логарифмическая спираль»
Самолет, вылетевший из какой-нибудь точки земного шара на север, через некоторое время окажется над Северным полюсом. Если же он полетит на восток, то, облетев параллель, вернется в тот же пункт, из которого вылетел. Предположим теперь, что самолет будет летать пересекая все меридианы под одним и тем же углом, отличным от прямого, т. е. держась все время одного и того же курса. Когда он облетит земной шар, то попадет в точку, имеющую ту же долготу, что и точка вылета, но расположенную ближе к Северному полюсу. После следующего облета он окажется еще ближе к полюсу и, продолжая лететь указанным образом, будет описывать вокруг полюса сужающуюся спираль.
Уравнение этой спирали r = 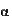 ek ek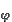 , ,
где r - расстояние от произвольной точки М на спирали до выбранной точки О,
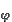 - угол между лучом ОМ и выбранным лучом Ох, - угол между лучом ОМ и выбранным лучом Ох, 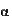 и k - постоянные. и k - постоянные.
Так как это уравнение связано с логарифмической функцией, то вычисленную по этой формуле спираль называют логарифмической.
 Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары, закручены по логарифмической спирали.
Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары, закручены по логарифмической спирали.
 Можно сказать, что эта спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг Гете считал ее даже математическим символом жизни и духовного развития.Очертания, выраженные логарифмической спиралью, имеют не только раковины, в подсолнухе семечки расположены по дугам, также близким к логарифмической спирали.
Можно сказать, что эта спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг Гете считал ее даже математическим символом жизни и духовного развития.Очертания, выраженные логарифмической спиралью, имеют не только раковины, в подсолнухе семечки расположены по дугам, также близким к логарифмической спирали.
Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали. По логарифмическим спиралям закручены и многие галактики, в частности, Галактика, которой принадлежит Солнечная система.
7. Любое число - тремя двойками.
Творческое задание.
Учитель: Продолжим урок остроумной алгебраической головоломкой, которой развлекались участники одного съезда физиков в Одессе. Некоторым учащимся на дом предлагалось творческое задание: число 3, целое и положительное, изобразить с помощью трех двоек и математических символов.
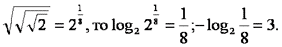

Задание 4.
Решите неравенство: logx + 0.5 (3 - x) > 1
Решение.
logx + 0.5(3 - x) > logx + 0.5(x + 0,5);
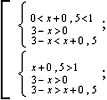  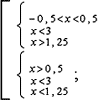 x
x 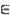 (0.5; 1.25). (0.5; 1.25).
IV. Домашнее задание (из вариантов ЕГЭ)
На «3» - 1), 2) и 3) задания; на «4» и на «5» - все задания.
1) Найти значение выражения: 5 * 5 log5 7;
2) Найти множество значений функции: y = 3 - log1/3x2;
3) Найти производную функции: y = 3.5x4 * e2x;
4) Найти корень уравнения (или сумму корней): log5 (2x + 33) - log5 13 = log5 x;
5) Найти произведения всех корней уравнения:  lg(7 - x - x2) = 0. lg(7 - x - x2) = 0.
V. Подведение итогов урока
Рефлексия
 В связи с чем возникла необходимость в логарифмах? В связи с чем возникла необходимость в логарифмах?
 Что нового вы узнали о логарифмической функции и ее приложениях? Что нового вы узнали о логарифмической функции и ее приложениях?
 Кого из учёных, внёсших вклад в развитие логарифмов, вы запомнили? Кого из учёных, внёсших вклад в развитие логарифмов, вы запомнили?
 Что надо учитывать, решая различные задания с логарифмами? Что надо учитывать, решая различные задания с логарифмами?
 Понравился ли вам сегодняшний урок? Понравился ли вам сегодняшний урок?
Литература:
1. Быков С.В., г. Брянск, школа №64. www.uroki.net
2. Зырянова С., г. Абинск. Еженедельная учебно-методическая газета "Математика", 1999г.
|
 "Логарифмическая функция и её приложения"
"Логарифмическая функция и её приложения" повторить свойства логарифмической функции;
повторить свойства логарифмической функции;
 обобщить, систематизировать и углубить знания по данной теме;
обобщить, систематизировать и углубить знания по данной теме;
 расширять представления учащихся о логарифмической функции, применении ее свойств в нестандартных ситуациях;
расширять представления учащихся о логарифмической функции, применении ее свойств в нестандартных ситуациях;
 развивать интерес к истории математики и ее практическим приложениям, логическое мышление, математическую грамотность речи;
развивать интерес к истории математики и ее практическим приложениям, логическое мышление, математическую грамотность речи;
 воспитывать познавательную активность, чувство ответственности, культуру общения, культуру диалога.
воспитывать познавательную активность, чувство ответственности, культуру общения, культуру диалога.






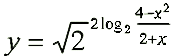
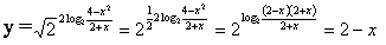 ОДЗ:
ОДЗ: 
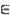 ( -
( - 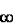 ; - 2 ) U (- 2; 2)
; - 2 ) U (- 2; 2)
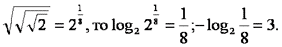

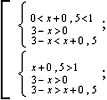

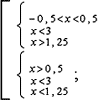 x
x 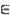 (0.5; 1.25).
(0.5; 1.25).
 lg(7 - x - x2) = 0.
lg(7 - x - x2) = 0.
 В связи с чем возникла необходимость в логарифмах?
В связи с чем возникла необходимость в логарифмах?
 Что нового вы узнали о логарифмической функции и ее приложениях?
Что нового вы узнали о логарифмической функции и ее приложениях?
 Кого из учёных, внёсших вклад в развитие логарифмов, вы запомнили?
Кого из учёных, внёсших вклад в развитие логарифмов, вы запомнили?
 Что надо учитывать, решая различные задания с логарифмами?
Что надо учитывать, решая различные задания с логарифмами?
 Понравился ли вам сегодняшний урок?
Понравился ли вам сегодняшний урок?
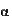 ,
,
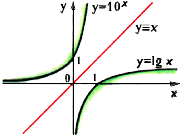

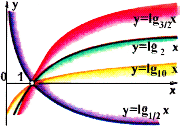
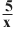 ;
;

 ; +
; +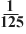 ; log327; log77; log51; ; lg0,0001; lg100000. (7, -3, 3, 1, 0, -4, 5)
; log327; log77; log51; ; lg0,0001; lg100000. (7, -3, 3, 1, 0, -4, 5)
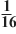 ; log464; log31; lg10; lg0,001; lg1000000. (5, -4, 2, 0, 1, -3, 6)
; log464; log31; lg10; lg0,001; lg1000000. (5, -4, 2, 0, 1, -3, 6)
 Еще недавно трудно было представить инженера без логарифмической линейки в кармане; изобретенная через десяток лет после появления логарифмов Непера английским математиком Гунтером, она позволяла быстро получать ответ с достаточной для инженера точностью в три значащие цифры. Теперь ее из инженерного обихода вытеснили микрокалькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни калькуляторы.
Еще недавно трудно было представить инженера без логарифмической линейки в кармане; изобретенная через десяток лет после появления логарифмов Непера английским математиком Гунтером, она позволяла быстро получать ответ с достаточной для инженера точностью в три значащие цифры. Теперь ее из инженерного обихода вытеснили микрокалькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни калькуляторы.

 Известный физик Эйхенвальд вспоминал: «Товарищ мой по гимназии любил играть на рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом не имеют ничего общего. «Правда, Пифагор нашел какие-то соотношения между звуковыми колебаниями, - но ведь как раз пифагорова-то гамма для нашей музыки и оказалась неприемлемой». Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах...»
Известный физик Эйхенвальд вспоминал: «Товарищ мой по гимназии любил играть на рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом не имеют ничего общего. «Правда, Пифагор нашел какие-то соотношения между звуковыми колебаниями, - но ведь как раз пифагорова-то гамма для нашей музыки и оказалась неприемлемой». Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах...»
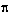 x log3(
x log3(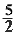 x - x 2) = 0 (Пшукова Назират)
x - x 2) = 0 (Пшукова Назират)
 ОДЗ
ОДЗ
 0
0 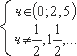
 +
+  + k; x
+ k; x 
 Астрономы делят звезды по степени яркости на видимые и абсолютные звездные величины - звезды первой величины, второй, третьей и т. д. Последовательность видимых звездных величин, воспринимаемых глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону: яркости звезд составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой логарифм ее физической яркости. Короче говоря, оценивая яркость звезд, астроном оперирует таблицей логарифмов, составленной при основании 2,5.
Астрономы делят звезды по степени яркости на видимые и абсолютные звездные величины - звезды первой величины, второй, третьей и т. д. Последовательность видимых звездных величин, воспринимаемых глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону: яркости звезд составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой логарифм ее физической яркости. Короче говоря, оценивая яркость звезд, астроном оперирует таблицей логарифмов, составленной при основании 2,5.
 >
>  , бесспорно правильного. Затем следует
преобразование, тоже не внушающее сомнения. Большему числу соответствует больший логарифм,
, бесспорно правильного. Затем следует
преобразование, тоже не внушающее сомнения. Большему числу соответствует больший логарифм,
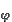 ,
, Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары, закручены по логарифмической спирали.
Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары, закручены по логарифмической спирали.
 Можно сказать, что эта спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг Гете считал ее даже математическим символом жизни и духовного развития.Очертания, выраженные логарифмической спиралью, имеют не только раковины, в подсолнухе семечки расположены по дугам, также близким к логарифмической спирали.
Можно сказать, что эта спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг Гете считал ее даже математическим символом жизни и духовного развития.Очертания, выраженные логарифмической спиралью, имеют не только раковины, в подсолнухе семечки расположены по дугам, также близким к логарифмической спирали.