Ход урока
1. Вступительное слово
Мы привыкли пользоваться благами цивилизации - автомобилем, телефоном, телевизором, компьютером и прочей техникой, делающей нашу жизнь легче и интереснее. Тысячи изобретений понадобилось для этого, но самым важным из них были первые - колесо и число. Без них не было бы всего нашего технического прогресса. У этих двух изобретений есть общая черта - ни колеса, ни числа нет в природе, и то и другое - плод деятельности человеческого разума.
Казалось бы, что понятие числа должно возникнуть одновременно с умением считать, но это далеко не так. Замечено, что считать до пяти умеют и кошки и свиньи, но чтобы перейти от пяти предметов к числу «пять», требовалось великое открытие. У некоторых древних племён имелись разные способы счета : для людей, для животных и для неодушевленных предметов. То есть уже тогда люди понимали, что три ребенка, три ореха и три козы - это не одно и тоже, но вместе с тем они обладают общим свойствам - их количество равно трём.
Итак, появились числа 1, 2, 3, ..., которыми можно выразить количество коров, деревьев, людей и т.д. Эти числа впоследствии получили название натуральные. Гораздо позднее появился ноль.
Однако ремесленникам и торговцам этих чисел было мало, поскольку возникали задачи деления на части. Так появились дроби и правила с ними.
Теперь торговцам и ремесленникам чисел было уже достаточно, но ещё математики Древней Греции, ученики знаменитого Пифагора, обнаружили, что есть числа, которые не выражаются никакой дробью. Первым таким числом стала длина диагонали квадрата, сторона которого равна единице. Это так поразило пифагорейцев, что они долгое время держали открытие в тайне. Новые числа стали называть иррациональными - недоступными пониманию, а целые числа и дроби - рациональными числами.
На этом история числа не окончилась. Математики ввели отрицательные числа, которые оказались удобными при решении многих задач. Казалось бы, уже все, но в ряде случаев возникает потребность найти число, квадрат которого равен минус единице. Среди известных чисел такого не оказалось, поэтому его назвали мнимой единицей. И появились новые числа - мнимые и комплексные. Сначала многие математики не признавали комплексные числа, пока не убедились в том, что с их помощью можно решать многие технические задачи, которые до этого не поддавались решению. С этими числами вы познакомитесь, если будете изучать высшую математику.
 Сегодня мы поговорим об одном из загадочных чисел в математики. Это число
Сегодня мы поговорим об одном из загадочных чисел в математики. Это число  . Его история начинается 4000 лет назад. Эти данные появились у человечества, когда исследователи известной пирамиды Хеопса усмотрели в отношениях её размеров заметные следы этого великого числа. А, именно, частное, полученное от деления суммы двух сторон на высоту, выражается числом 3,1416 - это значит числом
. Его история начинается 4000 лет назад. Эти данные появились у человечества, когда исследователи известной пирамиды Хеопса усмотрели в отношениях её размеров заметные следы этого великого числа. А, именно, частное, полученное от деления суммы двух сторон на высоту, выражается числом 3,1416 - это значит числом  с точностью до трех знаков после запятой. Но на протяжении этих 4000 лет
с точностью до трех знаков после запятой. Но на протяжении этих 4000 лет  претерпело много изменений. Об этом мы сегодня и поговорим на нашей конференции.
претерпело много изменений. Об этом мы сегодня и поговорим на нашей конференции.
2. Опыт «Простейшее вычисление»
В курсе геометрии 9 класса мы изучали теорему:
«Отношение длины окружности к её диаметру не зависит от окружности, т.е. одно и то же для любых двух окружностей».
Отношение длины окружности к её диаметру и есть число  . Эту теорему мы будем использовать при проведении опыта.
. Эту теорему мы будем использовать при проведении опыта.
Опыт: Надо взять цилиндрический сосуд и нить. Нитью надо «опоясать» сосуд и измерить её длину. Длина нити будет приблизительно равна длине окружности сосуда. Измерить диаметр сосуда. Найти частное от деления длины нити на диаметр. Получившееся число будет приблизительным значением числа  .
.
Итоги: длина окружности 12,5 см, длина диаметра 4 см,
 = 12,5 : 4 = 3,125. Число
= 12,5 : 4 = 3,125. Число  получено с точностью до десятых.
получено с точностью до десятых.
3. Опыт «Измерение с помощью взвешивания»
1) На листе картона надо начертить квадрат. Вписать в него круг. Вырезать квадрат и определить его массу с помощью школьных весов. Затем вырезать из квадрата круг и взвесить его.
2) Из физики известны следующие формулы :
m = dV, V = Sh, где d - плотность картона, h - толщина картона, S - площадь фигуры.
Для квадрата : Vкв = Sквh и Sкв= 4 R2 (где R радиус вписанной в него окружности). Значит mкв = d 4R2 h.
Для круга : Sкр =  R2 и Vкр =
R2 и Vкр =  R2 h. Значит mкр = d
R2 h. Значит mкр = d  R2 h.
R2 h.
| Отношение масс квадрата и круга: | 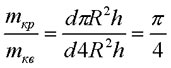 |
Отсюда  = = |
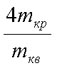 |
3) Пример: масса квадрата  54 г, масса круга
54 г, масса круга  42 г, отсюда
42 г, отсюда

 4 х 42 / 54
4 х 42 / 54  3,111…
3,111…
4. Программа вычисления числа 
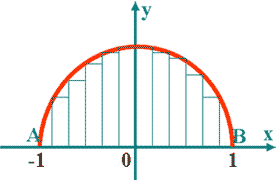
В курсе алгебры 11 класса в теме «Площадь криволинейной трапеции» мы использовали способ нахождения площади фигуры суммированием площадей прямоугольников, на которые разбивается данная фигура. Этим способом воспользуемся, чтобы найти число  .
.
В системе координат отметим точки А (-1; 0) и В(1;0). Опишем на АВ полуокружность как на диаметре. Разделим отрезок АВ на n равных частей точками х1, х2, ... , хn-1 и восстановим из них перпендикуляры до пересечения с полуокружностью. Длина каждого такого перпендикуляра – это значение функции
f(x) = 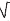 1-x2 (из уравнения окружности с центром в начале координат х2 + у2 = R2 и R = 1).
1-x2 (из уравнения окружности с центром в начале координат х2 + у2 = R2 и R = 1).
Построим на каждом перпендикуляре прямоугольник. Тогда площадь полукруга приблизительно будет равна сумме площадей этих прямоугольников, т.е. S = (2/n)* f(х0) + (2/ n)* f(х1) + ... + (2/ n)* f(xn-1) = (2/ n)*(f(x0) + f(x1)+ ... + f(xn-1)), где 2/ n - длина отрезка, на которые разделен отрезок АВ.
Площадь круга находится по формуле S =  R2, тогда площадь полукруга равна
R2, тогда площадь полукруга равна  R2 /2. В нашем случае R=1 и площадь полукруга равна
R2 /2. В нашем случае R=1 и площадь полукруга равна  / 2, т. е. S =
/ 2, т. е. S =  / 2 и отсюда
/ 2 и отсюда  = 2S = 2* (2/ n)*(f(x0) + f(x1)+ ... + f(xn-1)) = (4/ n)*(f(x0) + f(x1)+ ... + f(xn-1)).
= 2S = 2* (2/ n)*(f(x0) + f(x1)+ ... + f(xn-1)) = (4/ n)*(f(x0) + f(x1)+ ... + f(xn-1)).
Программа
Указания к программе:
1) сумму f(x0) + f(x1)+ ... + f(xn-1) обозначим буквой А;
2) длину отрезка, на которые разбивается отрезок АВ при делении на n равных час-тей, обозначим буквой D, т.е. D = 2 / n;
3) n - количество отрезков разбиения АВ - вводимая в программу величина;
4) значение суммы находится в цикле от -1 до 1с шагом равным D, первоначальное значение А будет равно 0;
5) число  обозначим буквой Р;
обозначим буквой Р;
6) согласно введенным обозначениям число  находиться по формуле :
находиться по формуле :
Р= (4/ n)*(f(x0) + f(x1)+ ... + f(xn-1)) = 2 * D *А и выводим на печать.
PRINT «Вычисление числа  методом прямоугольников»
методом прямоугольников»
INPUT «Введите число отрезков разбиения »; N
D = 2 / N
А = 0
FOR Х = -1 ТО 1 SТЕР D
A = A + SQR (1 – X^2)
NEXT X
Р = 2 * D *А
PRINT «Число  приблизительно равно »; Р
приблизительно равно »; Р
END
Итоги работы программы для различных значений:
1) N = 10  = 3, 0370488330990893;
= 3, 0370488330990893;
2) N = 100  = 3, 1387023562983739;
= 3, 1387023562983739;
3) N = 1000  = 3,1414874770234411;
= 3,1414874770234411;
4) N = 10 000  = 3, 1415893274326691;
= 3, 1415893274326691;
5) N = 100 000  = 3, 1415908253849745;
= 3, 1415908253849745;
6) N = 1 000 000  = 3, 1415925484070257.
= 3, 1415925484070257.
При N = 1 000 000 программа работала около 7 часов.
Немного истории ...
 Архимед в III в. до н.э.
обосновал в своей
небольшой работе
"Измерение круга" три положения:
Архимед в III в. до н.э.
обосновал в своей
небольшой работе
"Измерение круга" три положения:
1. Всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
2. Площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
3. Отношение любой окружности к её
диаметру меньше 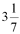 и больше и больше 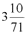
|
 Первым ввёл обозначение отношения
длины окружности к диаметру
современным символом
Первым ввёл обозначение отношения
длины окружности к диаметру
современным символом  английский математик
Уильман Джонсон в 1706 г. В качестве символа
он взял первую букву греческого слова
"periferia", что в переводе означает "окружность".
Введённое У. Джонсоном обозначение стало
общеупотребительным после опубликования
работ Л. Эйлера, который воспользовался
введённым символом впервые в 1736 г. английский математик
Уильман Джонсон в 1706 г. В качестве символа
он взял первую букву греческого слова
"periferia", что в переводе означает "окружность".
Введённое У. Джонсоном обозначение стало
общеупотребительным после опубликования
работ Л. Эйлера, который воспользовался
введённым символом впервые в 1736 г.
|


 54 г, масса круга
54 г, масса круга  42 г, отсюда
42 г, отсюда 
 4 х 42 / 54
4 х 42 / 54  3,111…
3,111…


 методом прямоугольников»
методом прямоугольников»
 приблизительно равно »; Р
приблизительно равно »; Р
 = 3, 0370488330990893;
= 3, 0370488330990893;
 = 3, 1387023562983739;
= 3, 1387023562983739;
 = 3,1414874770234411;
= 3,1414874770234411;
 = 3, 1415893274326691;
= 3, 1415893274326691;
 = 3, 1415908253849745;
= 3, 1415908253849745;
 = 3, 1415925484070257.
= 3, 1415925484070257.
 Общее развитие учащихся;
Общее развитие учащихся;  Сегодня мы поговорим об одном из загадочных чисел в математики. Это число
Сегодня мы поговорим об одном из загадочных чисел в математики. Это число 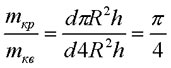
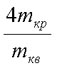
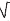 1-x2 (из уравнения окружности с центром в начале координат х2 + у2 = R2 и R = 1).
1-x2 (из уравнения окружности с центром в начале координат х2 + у2 = R2 и R = 1).
 Архимед в III в. до н.э.
обосновал в своей
небольшой работе
"Измерение круга" три положения:
Архимед в III в. до н.э.
обосновал в своей
небольшой работе
"Измерение круга" три положения:
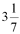 и больше
и больше 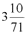
 Первым ввёл обозначение отношения
длины окружности к диаметру
современным символом
Первым ввёл обозначение отношения
длины окружности к диаметру
современным символом