|
«Вероятность и статистика»  Проверить знания учащихся по теме «Вероятность и статистика»; Проверить знания учащихся по теме «Вероятность и статистика»;
 Развить логическое мышление учащихся, грамотность математической речи; Развить логическое мышление учащихся, грамотность математической речи;
 Воспитывать ответственное отношение к труду. Воспитывать ответственное отношение к труду.
I. Организационно-психологический момент
На общественный смотр приглашены учителя школьного методического объединения учителей математики, родители учащихся, классный руководитель.
 У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1) У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1)
 Фронтальный опрос оставшихся учащихся; (вопросы к опросу в приложении №2);
( за правильный ответ каждый получает жетон). Фронтальный опрос оставшихся учащихся; (вопросы к опросу в приложении №2);
( за правильный ответ каждый получает жетон).
 Затем все слушают ответы учащихся первой пятерки. Затем все слушают ответы учащихся первой пятерки.
 У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1) У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1)
 Оставшиеся учащиеся решают самостоятельную работу: Оставшиеся учащиеся решают самостоятельную работу:
Проверка решения задач I и II вариантов через готовое решение на интерактивной доске;
Затем все слушают ответы учащихся второй пятерки.
 У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1) У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1)
 Устно: решить задачи с помощью интерактивной доски (приложение №4); Устно: решить задачи с помощью интерактивной доски (приложение №4);
 Затем все слушают ответы учащихся третьей пятерки. Затем все слушают ответы учащихся третьей пятерки.
 У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1) У доски готовятся к ответам по билетам 5 учащихся. (билеты в приложении №1)
 Словарный диктант для оставшихся учащихся; (вопросы к опросу в приложении №3);
( за правильный ответ каждый получает жетон). Словарный диктант для оставшихся учащихся; (вопросы к опросу в приложении №3);
( за правильный ответ каждый получает жетон).
 Затем все слушают ответы учащихся четвертой пятерки. Затем все слушают ответы учащихся четвертой пятерки.
 Жюри проверяет диктант и подводит итоги; Жюри проверяет диктант и подводит итоги;
 Пока жюри подводит итоги учащимся предлагается закончить фразу: «Вероятность и статистику нужно знать…» Пока жюри подводит итоги учащимся предлагается закончить фразу: «Вероятность и статистику нужно знать…»
Приложение № 1 Билет № 1.1. Понятие множества, его элементов. Способы задания множеств. 2. Теорема о выборках двух элементов Билет № 2. 1. Определение подмножества. Примеры. 2. Число сочетаний из n элементов по2. Билет № 3. 1. Пересечение множеств. Примеры. 2. Число сочетаний из n элементов по k. Билет № 4. 1. Объединение множеств. Примеры. 2. Теорема о выборах трех элементов. Билет № 5. 1. Комбинаторные задачи. Понятие. Примеры. 2. Таблица распределения частот выборки. Билет № 6. 1. Правило умножения испытаний. 2. График распределения выборки. Билет № 7. 1. Дерево возможных вариантов. Примеры. 2. Полигон частот. Билет № 8. 1. n! Определение. Теорема о перестановках элементов конечного множества. 2. Гистограмма распределения частот. Билет № 9. 1. Группировка информации. 2. Построение кривой нормального распределения. Билет № 10. 1. Табличное представление информации. 2. Числовые характеристики выборки. Билет № 11. 1. Графическое представление информации. 2. Схема Бернулли. Примеры. Билет № 12. 1. Числовые характеристики данных измерений. 2. Теорема Бернулли. Билет № 13. 1. Случайные события. Случайный эксперимент. Элементарные исходы. 2. Равновозможные события и подъем их вероятности. Билет № 14. 1. Вероятность. Определение. Классическая вероятность. 2. Числовые характеристики выборки. Билет № 15. 1. Противоположные события. Несовместные события. Определения. Примеры. 2. Объединение множеств. Примеры. Билет № 16. 1. Сумма событий. Теорема о сумме событий. 2. Переселение множеств. Примеры. Билет № 17. 1. Статистическая устойчивость. 2. Диаграммы Эйлера. Билет № 18. 1. Статистическая вероятность. 2. Числовые характеристики выборки. Приложение № 2 Вопросы для фронтального опроса1. Что составляет фундамент современного математического языка? 2. Что такое множество? Как оно обозначается? 3. Какие множества называются числовыми? 4. Какое множество называется пустым? Как оно обозначается? 5. Что такое элемент множества? Знак принадлежности. 6. Что такое подмножество? Как обозначается подмножество В множества А. 7. Какие круги называются кругами Эйлера? 8. Что называется пересечение множеств А и В. 9. Что называется объединением множеств А и В. 10. Какие события называются случайными? 11. Какие события называются невозможными? 12. Какие события называются достоверными? 13. Что такое случайный опыт? 14. Что такое абсолютная частота? 15. Что такое относительная частота? 16. Что такое вероятность? 17. Сформулируйте общую схему решения задач на классическую вероятность. 18. Сформулируйте правила умножения. 19. Что такое n! 20. Сформулировать теорему о перестановках элементов конечного множества. 21. Что такое полигон распределения данных? 22. Что такое гистограмма? 23. Что такое варианта? 24. Что называется размахом измерения? 25. Что называется модой измерения? 26. Что называется средним значением? Приложение № 3 ДиктантВероятность, статистика, подмножество, пересечение, объединение, факториал, полигон, гистограмма, диаграмма, равновозможное событие, несовместные события, кратность варианты, размах измерения. Приложение № 4 Задачи для устного решения1. По указанному заданию множества дать его словесное описание а) 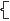 0,2,4,6,8 0,2,4,6,8 , ,
б) 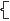 2,4,6,… 18,20 2,4,6,… 18,20 , ,
в) 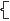 12,22,32, … 92 12,22,32, … 92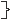 , ,
г) 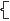 1,8, 27,64,125, … 1,8, 27,64,125, …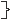
2. Найти пересечение А  В множеств А и В В множеств А и В
а) А = 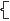 11, 22, …, 88,99 11, 22, …, 88,99
В = 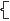 3,6,9, … 3,6,9, …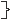
б) А= (1; 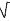 10), В = N 10), В = N
3. Найти объединение А 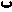 В множеств А и В В множеств А и В
а) А – множество делителей числа 105, В – множество делителей числа 55. б) А = (1; 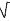 10), В = 10), В =  2; 4 2; 4
4. В 9б классе в среду семь уроков: алгебра, геометрия, литература, русский язык, биология, английский язык и физкультуры. Сколько можно составить вариантов расписания на среду? 5. Среди школьников седьмых классов был проведен выборочный опрос: из скольких человек состоят их семьи? В результате такого опроса была получена следующая выборка: 2 2 3 3 3 3 4 2 3 3 2 3 2 3 2 3 2 4 3 2 2 3 2 4 5 2 33 2 4 3 2 3 4 3 3 2 3 5 3. Составить таблицу распределения частот. 6. Найдите среднее арифметическое и моду числового ряда: 5, 8, 4, 9, 5, 2, 5 7. В автомобиле 5 мест. Сколькими способами пять человек могут занять места для путешествия, если водить машину могут только трое из них? Учитель математики МОУ «Гимназия №2» – Ворошилова И.М. | |||


